Our paper “Analytical mass transfer coefficients for natural convection from vertical gas-evolving electrodes” has been accepted for publication in the International Journal of Heat and Mass Transfer. In it, together with my colleague dr. Willem Haverkort, we derive a new analytical solution for the mass transfer coefficients between a vertical electrode and the bulk liquid, when we have laminar natural convection. The results are important for the design of electrolyzers, and electrochemical systems in general. The paper is available as open access here.
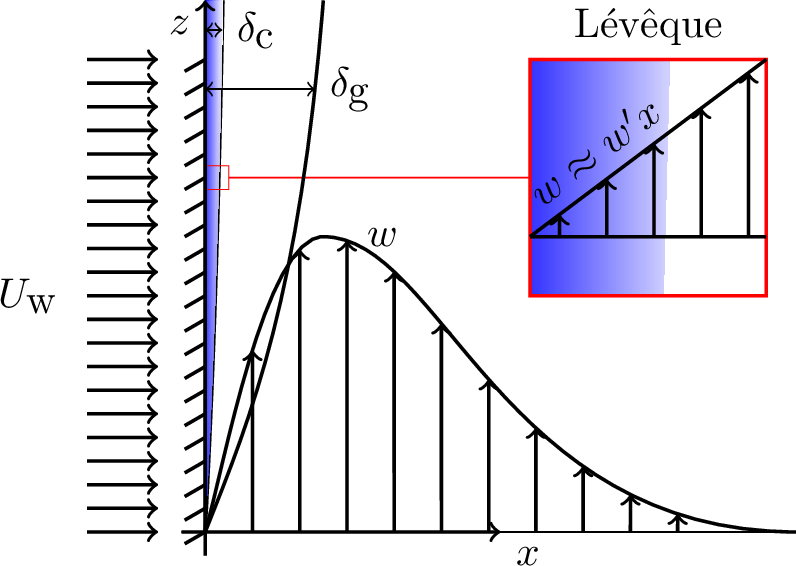
The first novelty is that we use a new self-similarity solution for the multiphase flows. We use the mixture model, which means that we treat the liquid and the bubbles as a single fluid with variable density and viscosity, and then use the Prandtl boundary layer equations to simplify the equations in the case of a laminar boundary layer.
The second novelty is that we consider both the case of constant concentration at the wall and, most remarkably, the less explored one of constant flux, which is nonetheless the most relevant one for electrochemical systems. We solve the mass transfer problem using the Lévêque approximation (i.e.: linearizing the velocity profile near the electrode), which is valid for high Schmidt numbers (typical for aqueous solutions of gaseous species).
Finally, the model is compared with experimental results from the literature, showing excellent agreement between theory and experiments. In addition, the model recovers the result for classical thermal convection. If you want to read more about it, I encourage you to read it here.